
P-values are most often used by researchers to say whether a certain pattern they have measured is statistically significant. No matter what test you use, the p-value always describes the same thing: how often you can expect to see a test statistic as extreme or more extreme than the one calculated from your test.

To compare three different diets, use an ANOVA instead – doing multiple pairwise comparisons will result in artificially low p-values and lets you overestimate the significance of the difference between groups. The number of independent variables you include in your test changes how large or small the test statistic needs to be to generate the same p-value.Įxample: Choosing a statistical testIf you are comparing only two different diets, then a two-sample t-test is a good way to compare the groups.You should choose the statistical test that best fits your data and matches the effect or relationship you want to test. Different statistical tests have different assumptions and generate different test statistics.The calculation of the p-value depends on the statistical test you are using to test your hypothesis: These tables show, based on the test statistic and degrees of freedom (number of observations minus number of independent variables) of your test, how frequently you would expect to see that test statistic under the null hypothesis.
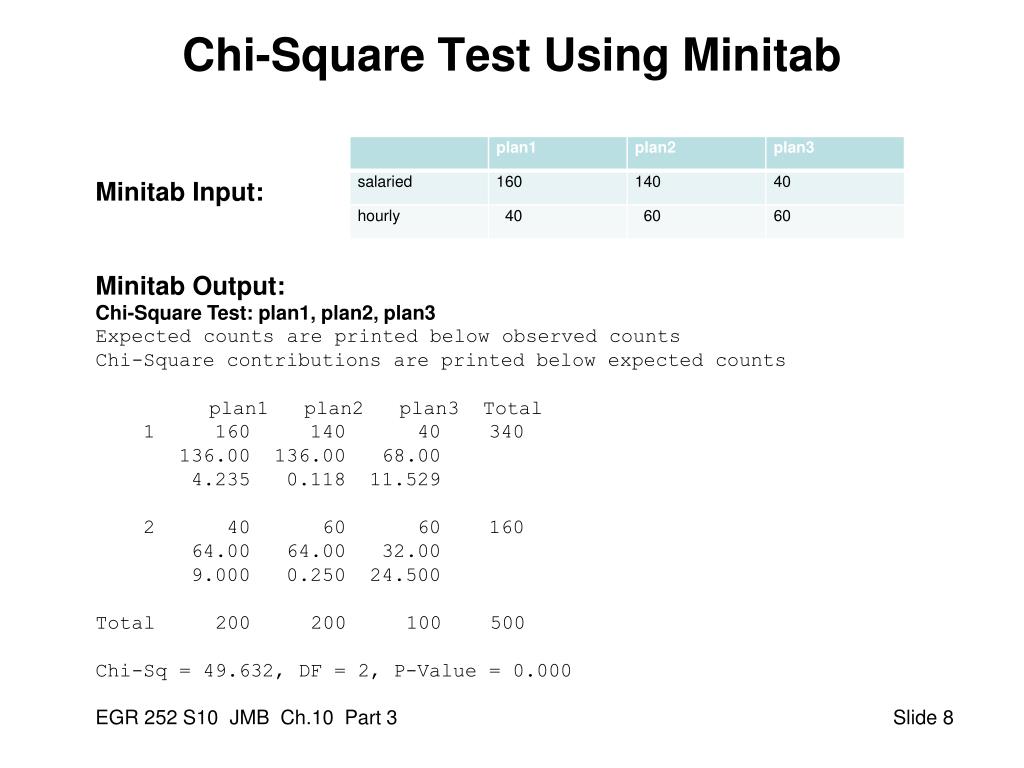
You can also find tables for estimating the p-value of your test statistic online. P-values are usually automatically calculated by your statistical program (R, SPSS, etc.). The p-value will never reach zero, because there’s always a possibility, even if extremely unlikely, that the patterns in your data occurred by chance. If, however, there is an average difference in longevity between the two groups, then your test statistic will move further away from the values predicted by the null hypothesis, and the p-value will get smaller. It likely won’t reach exactly 1, because in real life the groups will probably not be perfectly equal. Example: Test statistic and p-valueIf the mice live equally long on either diet, then the test statistic from your t-test will closely match the test statistic from the null hypothesis (that there is no difference between groups), and the resulting p-value will be close to 1. The p-value is a proportion: if your p-value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was true. The p-value gets smaller as the test statistic calculated from your data gets further away from the range of test statistics predicted by the null hypothesis. The p-value tells you how often you would expect to see a test statistic as extreme or more extreme than the one calculated by your statistical test if the null hypothesis of that test was true. It does this by calculating the likelihood of your test statistic, which is the number calculated by a statistical test using your data.

The p -value, or probability value, tells you how likely it is that your data could have occurred under the null hypothesis.
The test statistic can be translated into a p-value. A p-value is the probability of chance alone producing the value of our test statistic under the assumption that the null hypothesis is true. The type of statistic that we use depends upon the particular test that we are conducting. The calculation relies upon our statistical sample. The alternative hypothesis may involve a one-sided or a two-sided test. We should also determine the level of significance, which will be denoted by the Greek letter alpha.


 0 kommentar(er)
0 kommentar(er)
